9-А клас Геометрія дистанційне навчання 2019/2021
ІІ семестр 2020-2021 н.р.
2. Уважно прочитайте § 24 та виконайте запитання і завдання самоконтролю:
На минулому уроці ми сформулювали основні ідеї розв'язування трикутників:
- як у довільному трикутнику знайти невідому сторону,
якщо ми знаємо дві сторони і кут між ними?
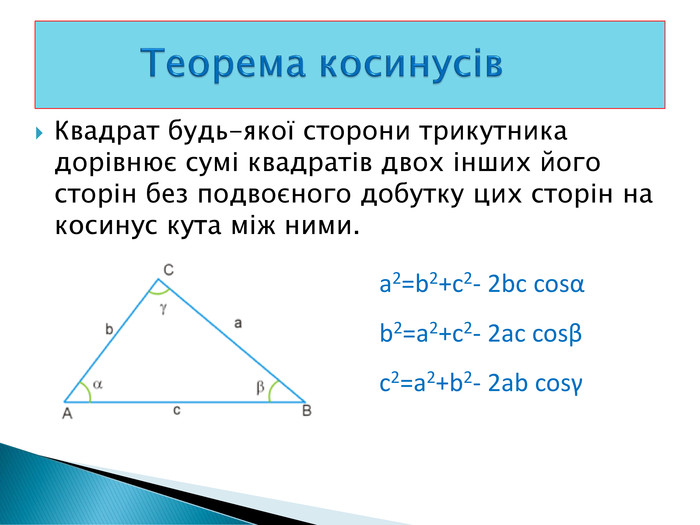
На допомогу приходить теорема косинусів:
Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток цих сторін трикутника
і косинуса кута між ними.
Нагадаю,що за допомогою теореми косинусів, ми можемо
не тільки знаходити невідому сторону трикутника,
коли відомі дві його сторони та кут між ними.
Теорема косинусів може стати у пригоді, коли потрібно знайти кути трикутника, якщо відомі всі його сторони.
Але й це ще не все.
Теорема косинусів може бути корисною для визначення,
гострокутним, тупокутним чи прямокутним є цей трикутник.
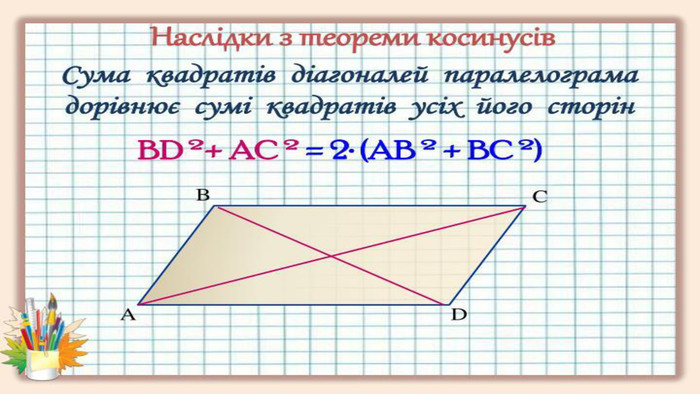
За допомогою теореми косинусів доводиться цікавий факт про паралелограм.
Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.
Домашнє завдання:
п. 13 № 429, 431, 446
13 січня
Теорема косинусів. Урок 1.
Залящева Юлія |
Кармазіна Олена |
Карманний Дмитро |
Ковтун Дмитро |
Корнілова Єва |
Кружилін Ілля |
Литвин Артем |
Логушов Владислав |
Навродський Кирило |
Назаренко Анастасія |
Нестеренко Владислав |
Оганісян Каріне |
Оганісян Юлія |
Павленко Анастасія |
Підгорний Тимофій |
Поліщук Дмитро |
Придворова Юлія |
Рибчак Анастасія |
Савенко Валерія |
Соколова Анастасія |
Томілов Дмитро |
Чабан Софія |
Черномаз Олександра |
Чугун Дмитро |
1. Повторення вивченого. Завдання виконати в зошиті.
Якщо A(x1;y1) і B(x2;y2) - дві довільні точки і C(x;y) середина відрізка AB. Тоді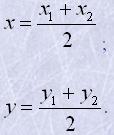
Якщо A(x1;y1) і B(x2;y2) - дві довільні точки, то відстань між точками A і B обчислюється за формулою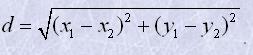
Приклад 1
Знайдіть довжину d відрізка AB та координати його середини C, якщо відомі координати точок A і B: A(1;-6), B(4;-2).
Розв'язання
Довжина відрізка AB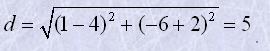
завдання:
1. Знайти координати середини відрізка з кінцями (2;0) і (0;2).
2.Дано один кінець відрізка (1;1) і його середину (2;2). Знайти другий кінець відрізка.
3.Дано дві точки: A(5;-2), B(2;2), Знайти відстань між цими точками.
4.Дано три точки: A(4;-2), B(1;2), C(-2;6). Знайти відстань між цими точками, взятими попарно.
2. Рівняння кола
Рівняння кола з центром у точці Q(а; b) радіусом r має вигляд (мал. 299)
Зокрема, рівняння кола радіуса r з центром у початку координат має вигляд х2 + у2 = r2.
Приклад 1. Визначте центр та радіус кола, заданого рівнянням (x + 3)2 + (у - 2)2 = 36.
Розв’язання. Маємо (х - (- 3))2 + (у - 2)2 = 62. Отже, центром кола є точка Q(-3; 2), а радіус кола r = 6.
Приклад 2. Довести, що рівняння х2 + у2 - 6х + 4у - 12 = 0 є рівнянням кола. Знайдіть координати центра кола та його радіус.
Розв’язання. Виділимо квадрати лінійних двочленів змінних х і у:

Отже, задане рівняння є рівняння кола з центром у точці Q(3; -2) і радіус r = 5.
Приклад 3. Складіть рівняння кола з діаметром АВ, якщо А(-6; 8), В(4; 12).
Розв’язання.
1) Нехай точка Q - центр кола. Тоді Q - середина АВ. Маємо:

Отже, Q(-1; 10).
2) Радіусом кола буде відрізок  Отже, r =
Отже, r = ![]() .
.
3) Рівняння шуканого кола таке:

Виконати завдання: с. 41, № 160, 163
Тема уроку. Прямокутна система координат на площині.
Повторимо матеріал, пов'язаний з координатною площиною, відомий вам з курсу математики 6 класу та алгебри 7 і 8 класів:
1. Що називається прямокутною системою координат? рис. 126
2. Як у прямокутній системі координат називають горизонтальну пряму Ох; вертикальну пряму Оу; точку О(0; 0)?
3. Що таке абсциса точки? ордината точки?
4. Назвіть абсцису та ординату точки: А(2; 1), В(-1; 2), С(-2; -1), D(1; -2).
5. Прочитайте: A(3; 4), В(-2; 5), С(2; -2), D(0; 3).
6. Запишіть координати точок, зображених на рис. 127, і вкажіть, у яких координатних чвертях вони розміщені.
7. Що можна сказати про координати точки, яка лежить на осі абсцис? на осі ординат?
8. Накресліть в зошиті прямокутну систему координат та побудуйте точки:
А(3; 0), В(3; 4), С(-3; -2), D(-4; 0), E(3; -2), F(-3; 2).
Запам'ятай!
Щоб задати систему координат на площині означає, що кожній точці площини можна поставити у відповідність впорядковану пару дійсних чисел х і у і, навпаки, кожній парі х і у — єдину точку площини.
Виконання вправ
1. У яких точках на координатній площині дорівнюють нулю абсциси? ординати?
2. Де розташовані на координатній площині точки, абсциси яких дорівнюють 5? ординати яких дорівнюють -5?
3. Побудуйте на координатній площині чотирикутник ABCD,
якщо А(-3; 2), В(3; 2), С(-3; -1), D(3; -1). Визначте вид чотирикутника, знайдіть периметр і площу цього чотирикутника.
4. Нехай А(-5; -1), В(-1; -1), С(-1; -3) — координати трьох вершин прямокутника. Знайдіть координати четвертої вершини. Чому дорівнюють периметр і площа цього прямокутника?
5. Дано точку А(2; 3). Знайдіть координати основи перпендикуляра, опущеного з точки А на вісь Ох; на вісь Оу.
6. Де на координатній площині розташовані всі точки, абсциси яких дорівнюють їх ординатам?
7. Побудуйте на координатній площині всі точки з абсцисою х і ординатою у такі, що:
а) |x| = 3, |у| = 2; б) |x| = 3, |у| ≤ 2; в) |х| ≤ 3, |y| = 2; г) |x| ≤ 3, |у| ≤ 2.
8. При якому значенні х точки А(2x – 1; 0) і В(x + 1; 5) лежать на одній прямій, яка паралельна осі Оу?
9. Знайдіть площу трикутника з вершинами в точках А(0; 0), В(1; 2), С(3; 1).
Домашнє завдання
1. Повторити відомості про декартові координати на площині (параграф 3, ст. 24).
2. Виконати завдання.
1) Побудуйте квадрат ABCD так, щоб вершина С мала координати (-2; 2), а діагоналі квадрата перетиналися в початку координат. Знайдіть координати точок А, В, D та периметр і площу цього квадрата.
2) Зобразіть на координатній площині всі точки (х;у), якщо:
а) у = 0, х ≤ 2; б) -2 ≤ у ≤ 2, х ≥ 0; в) |x| ≤ 2, у ≥ 1; г) |х| ≥ 2, у ≤ -2.
3) Дано точку А(-3; 4). Укажіть координати основ перпендикулярів, які опущені з цієї точки на координатні осі. Чому дорівнює відстань від точки А до координатних осей? до початку координат?
Тема: Геометричні перетворення.
Симетрія відносно точки. Симетрія відносно прямої
2. Переглянути відео:
3. Перевір себе сам :
Вправа: Осьова симетрія,
Вправа: Симетрія ( не оцінюються)
4. Виконати на оцінку ТЕСТ " Симетрія"
( результат вашої роботи буде збережений, оцінка виставлена після карантину)
Тема: Симетрія відносно точки.
Симетрія відносно прямої
Поворот.
4. Виконати на оцінку ТЕСТ "Перетворення фігур. Переміщення"
Тема: Симетрія відносно точки.
Симетрія відносно прямої
Поворот.
Практична робота 1 :
Практична робота 3
Завдання з 06.04 по 13.04
Що таке паралельне перенесення
Розв'язування задач 1
Розв'язування задач 2
Практичні завдання на геометричні переміщення
Отже:
Точка М(х;у)-прообраз точки М'(х';у')


Вправа: Паралельне перенесення на координатній площині
Вправа: № 902
Вправа Формули паралельного перенесення
5. В робочих зошитах виконати практичну роботу.
Практична робота 4
6. Виконати на оцінку ТЕСТ "Паралельне перенесення"
Тема: Перетворення подібності.
3. Опрацювати презентацію:
4. Переглянути відео:
5. Перевір себе сам:
На повторення: Вправа Площі многокутників 1
Вправа Площі многокутників 2
Вправа Ознаки подібності трикутників
Вправа Ознаки подібності трикутників
6. В робочих зошитах виконати практичну роботу.
Практична робота 5
Screenshot ( або фото) виконаних ПРАКТИЧНИХ РОБІТ для перевiрки можна надiслати за адресою:
Тема: Гомотетія.
1. Вивчити за підручником після §26 Для допитливих : ст. 222-223 та перегляньте відео:
2. Ознайомитися з презентацією:
3.В робочих зошитах виконати практичну роботу.
Практична робота 6
Тема : Контрольна робота "Геометричні переміщення. Перетворення подібності"
ст. 6-57.
Відео:
Декартові координати на площині
ст. 57-103
2.Відео:
Вектори на площині
Сума та різниця векторів
Скалярний добуток двох векторів
Кут між векторами
Ознака колінеарності векторів
3. Виконати на оцінку ТЕСТ Повторення. Вектори на площині
ст. 107-143.
Теорема косинусів
Теорема синусів
Розв'язування трикутників
Площа трикутника
3. Виконати на оцінку ТЕСТ Розя'зування трикутників
4. Виконати на оцінку ТЕСТ Площі многокутників










Комментарии
Отправить комментарий