9-Б клас Алгебра дистанційне навчання 2019/2021

 05.05.Контрольна робота👈

(виконати до 07.05)

28.04.Підготовка до контрольної роботи.

Ознайомтеся із типовими завданнями до контрольної роботи на стор. 221. Виконайте завдання №1-8

26.04.Статистика

Уважно прочитайте приклади роз'язування задач § 21 та перевірте свої знання:

1. Що досліджує математична статистика? 

2. Що таке гістограма? 

3. Які явища називають масовими? 

4. Що таке вибірка? Частота вибірки? 

5. Назвіть центральні тенденції вибірки. 

6. Що таке середнє значення вибірки? медіана, мода?

3. Виконайте завдання № 856, 858, 861

21.04. Відомості про статистику.

1.Перегляньте відео

2. Виконайте вправи: №855,857

19.04.Частота та ймовірність випадкової події.Розв'язування вправ.

Перегляньте відео.

Виконайте вправи:№ 832,833,840

Онлайн урок: 19 апр. 2021 11:15  

Подключиться к конференции Zoom

https://us04web.zoom.us/j/77092016671?pwd=cnZDTnJQSVNNS2tmZ2c5STczVzduZz09

ІД: 770 9201 6671

Код : 1115

13.04.Класичне означення ймовірності

 

1. Події та їх ймовірності.

Завжди і всюди ми в своєму житті маємо справу з подіями: випав сніг, зустрілись люди, хтось виграв певну суму грошей в казино, а хтось програв...

Отже, первісне поняття, яким ми користуємось при вивченні навколишнього світу, -  це поняття події, яке не означається, а лише пояснюється.

Подія - це будь-який факт, що здійснюється або не здійснюється, тобто при певних умовах (комплексі умов) він може відбутися або не відбутися.

Кожне здійснення відповідного комплексу умов називається випробуванням: кидання монети на стіл, купівля лотерейного квитка тощо.

Теорія ймовірностей - математична наука, що вивчає закономірності  випадкових явищ.

Явище називається випадковим, якщо його перебіг передбачити неможливо. До випадкових явищ відносяться випадкові події, випадкові величини, випадкові функції та інше.

Спостерігаючи за різними випадковими явищами, інтуїтивно відчувається, що вони мають різну можливість появи в окремому випробуванні. Наприклад: якщо 10 раз підкинути монету, то з досить великою ймовірністю можна чекати появи хоча б одного герба; якщо ж 10 раз спробувати вгадати 6 чисел з 36 в лотереї , то з великою мірою впевненості можна говорити, що жодного разу не вгадаємо.

Випадкова подія - подія, яка в результаті випробування може відбутись, а може і не відбутись.

Випадкові події позначаються: А, В, С, D і т.д., тобто великими латинськими буквами.

Ймовірність випадкової події - це деяка чисельна міра об`єктивної можливості появи випадкової події, позначається Р(А).

 

Класичне означення ймовірності.

Ймовірність події А дорівнює відношенню числа випадків, що сприяють події А, до числа всіх можливих випадків, тобто , де n - число всіх можливих випадків, а m - число випадків, що сприяють події А.

0 < Р(А) < 1.

 

Розглядаючи різні випробування, ми ідеалізуємо умови, в яких вони проводяться. Наприклад: гральний кубик вважаємо кубом ідеальної форми, зробленим з речовини, густина якої  стала, центр куба знаходиться в точці перетину його діагоналей і т. д. Зрозуміло, що в цьому випадку поява 1 очка така ж, як поява 2, або 3, або 4, або 5, або 6 і дорівнює .

Розглядаються також події вірогідні ( достовірні ) і неможливі.

 

Вірогідною   називається подія, яка в результаті випробувань відбудеться завжди. Позначається U.

P(U)=1.

Наприклад: якщо число парне, то воно обов`язково поділиться на 2;

                 якщо підкинути гральний кубик, він обов`язково впаде на одну із граней і т. д.

 

Неможливою   називається подія, яка в результаті випробувань не може відбутись ніколи. Позначається V.

P(V)=0.

Наприклад: якщо число непарне, то воно ніколи не поділиться на 2; літак не може летіти із швидкістю світла, людина не може жити вічно і т. д.

Задача. З колоди 36 карт виймається одна карта. Яка ймовірність появи карти червової масті?
Розв'язок. Кількість елементарних фіналів (кількість карт) N=36. Подія A - поява карти червової масті. Число випадків, сприяють появі події A, N(A)=9. Отже, P(A)=936=14=0,25

12.04.Випадкова подія. Частота та ймовірність випадкової події.

Перегляньте відео.

Прочитайте параграф 20.

Виконайте вправи № 827,831

07.04. Розв'язування вправ.

Урок о 11:00  

Підключитися в Zoom

https://us04web.zoom.us/j/74811634820?pwd=Nm1QVm5MZ3BFUUlONjZrSTRkdldJQT09

Ід: 748 1163 4820

Код: 0704

Приклади розв'язання задач.

Виконайте: №803,808

05.04. Основні правила комбінаторики.

Мета: Ознайомитися з розділом математики про розвязування задач вибору та розташування елеметнтів деякої скінченної множини відповідно до заданих правил.

Завдання: Опрацювати параграф 19.

                Виконати №798,802

31.03.Контрольна робота з теми"Арифметична та геометрична прогресії"(виконати до 01.04.)

👉    Завдання до контрольної роботи.

 

29.03.Підготовка до контрольної роботи.

Повторіть:

2. Виконайте завдання.

20.01.Розв'язування квадратних нерівностей

1.Виконайте вправи: №12.7.(1,3,5,7,9),12.10.(1,2,4)

18.01.Розв'язування квадратних нерівностей методом інтервалів.

Онлайн урок 11:30  

https://us04web.zoom.us/j/71043086942?pwd=MzVoVk9vQ0hoQjNXMjJIQWxNMzNIQT09

Ід: 710 4308 6942

Код доступа: 1801

1. Завдання для повторення: -х² + 2х - 5 = 0, -х² + 2х – 5 < 0

Етапи методу інтервалів:
- знаходять корені квадратного тричлена ax2+bx+c і розкладають на множники;
- відзначають на числовій прямій корені тричлена і знаходять знаки квадратного тричлена на кожному інтервалі;
- обирають інтервал, відповідний знаку нерівності і записують відповідь.

Приклад:

Розв'язати нерівність. 2x2−7x−4≤0

Розв'язання. Знайдемо корені квадратного тричлена 2x2−7x−4 

і розкладемо його на множники за формулою ax2+bx+c=a(x−x1)(x+x1)

2x2−7x−4=0

Зазначимо на числовій прямій корені і знайдемо знаки квадратного тричлена на кожному інтервалі.
Для цього з кожного інтервалу достатньо взяти по одному значенню і підставити замість x у тричлен.

На інтервалі (−∞;−0,5] візьмемо x=−2, тоді 2⋅(−2)2−7⋅(−2)−4=2⋅4+14−4=18>0

 

На інтервалі [−0,5;4] візьмемо x=0, тоді 2⋅02−7⋅0−4=0−0−4=−4<0

 

На інтервалі  [4;+∞) візьмемо x=5, тоді 2⋅52−7⋅5−4=2⋅25−35−4=50−39=11>0

 

Квадратний тричлен приймає від'ємні і рівні нулю значення на інтервалі [−0,5;4].

Відповідь: −0,5≤x≤4 

 

х² - Зх + 2 > 0

 х² + 3х-4 < 0

3х² – 6х + 24 < 0.

Д/з. №487(б,г,д),496 (а,б,в).

13.01.Розв'язування квадратних нерівностей.

Время: 11:30 

Подключиться: https://us04web.zoom.us/j/79231848015?pwd=R1l4LzJ6ci83dXFiRC9xWm84TXMvdz09

Идентификатор конференции: 792 3184 8015

Код доступа: 1133

Загальний вигляд квадратних нерівностей, це ax2+bx+c>0(<0,≤0,≥0),деa≠0.

Множину розв'язків квадратної нерівності легко визначити, приблизно накресливши графік функції y=ax2+bx+c (параболу).

 

Кроки розв'язання квадратної нерівності:

 

1. Визначаються точки перетину параболи і осі x за допомогою розв'язання рівняння ax2+bx+c=0.

 Згадаємо формули коренів квадратного рівняння:

 D=b2−4acx1=−b+D−−√2a,x2=−b−D−−√2a

 

Якщо  D>0, у рівняння два різних кореня, парабола перетинає вісь x у двох точках
Якщо  D=0, у рівняння два однакових кореня, вершина параболи знаходиться на осі x
Якщо  D<0, у рівняння немає коренів, парабола не перетинає вісь x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

2. Враховуючи кількість коренів і знак коефіцієнта a, креслиться графік параболи.

Зверни увагу!

Якщо a>0, гілки параболи спрямовані вгору, якщо a<0, тоді вниз.

 

Порада: якщо хочеш, щоб гілки параболи завжди були спрямовані вгору, у випадках, коли a<0, треба спочатку обидві частини нерівності помножити на (−1). Не забудь, що на протилежний поміняється знак нерівності.

 

3. Обираються порожні або зафарбовані точки, в залежності від вигляду знака нерівності:

∙, якщо стоїть знак нестрогої нерівності ≤ або  ≥

о, якщо стоїть знак строгої нерівності < або <

 

4. Зафарбовується правильний інтервал.

 

5. Записується відповідь.

Приклад:

Розв'язати квадратну нерівність −2x2+4x−5≤0

Розв'язання:

−2x2+4x−5≤0∣∣⋅(−1)2x2−4x+5≥0D=16−4⋅2⋅5=−24парабола не перетинає вісьOx   За малюнком видно, що графік додатний будь-якому значенню x   Відповідь:  x∈(−∞;+∞)абоx∈R

Д/З. № 

11.01.Квадратні нерівності

Время: 11 янв. 2021 11:30 AM Киев

Підключитися

https://us04web.zoom.us/j/78491601173?pwd=WGNaTmI3V0c5MW4reU1CQVY1U0RVdz09

Идентификатор конференции: 784 9160 1173

Код доступа: 1123

№ 481 (г,д), 482

2312. Повторення. Розв"язування квадратних рівнянь. 

21.12.Квадратична функція та її графік.

Перевірьте свої знання виконавши тест☝

18.11. Функції. Властивості функції.

№ 301,303.

16.11.Функції. Властивості функції.

 Время: 16 ноя 2020 11:15 AM Киев

Подключиться к конференции Zoom

https://us04web.zoom.us/j/78240583757?pwd=RXZOUDJ0WGltOVQzZFI5eHB5UmgwZz09

Идентификатор конференции: 782 4058 3757

Код доступа: 1616

02.11.Тема уроку. Розв'язування систем лінійних нерівностей з однією змінною.

1.     Поняття системи нерівностей з однією змінною та її розв’язку. Якщо доводиться знаходити спільні розв'язки двох або більшої кількості нерівностей з однією і тією самою змінною, то кажуть, що ці нерівності утворюють систему нерівностей. Систему нерівностей позначають фігурною дужкою: Розв'язок системи нерівностей – це значення змінної, яке задовольняє кожну нерівність системи. Розв'язати систему нерівностей – означає знайти всі її розв'язки або показати, що вона їх немає.  2.     Схема розв'язування систем лінійних нерівностей з однією змінною:        I.            Розв'язуємо кожну нерівність системи;  II. Зображуємо множину розв'язків кожної нерівності на одній координатній прямій;  III.   Знаходимо переріз множини розв'язків нерівностей і записуємо множину розв'язків системи у вигляді проміжку або відповідної нерівності.  3.     Розв'язування систем лінійних нерівностей з однією змінною.

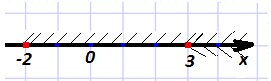
Приклад. Розв'яжемо систему нерівностей

   

Розв'язок кожної з нерівностей системи є числовим проміжком, відповідно (3; +∞) і (-2; +∞).

Запис (3; +∞) Ç (-2; +∞) означає переріз, тобто спільну частину даних проміжків.

Розв'язком нерівності є проміжок (3; +∞).

 Д/З. №221, 222

07.10.2020

Розвязування нерівностей з однією змінною.

 Нерівністю зі змінною (невідомим) називають два вирази зі змінною (невідомим), між якими стоїть один зі знаків нерівності: > (більше), < (менше), ≥ (більше або дорівнює; не менше); ≤ (менше або дорівнює; не більше).

Розв’язком нерівності з однією змінною називають значення змінної, яке перетворює нерівність на правильну числову нерівність.

 Розв’язати нерівність з однією змінною означає знайти всі її розв’язки або довести, що розв’язків немає.

     Розв’язками нерівності є деяка множина чисел.

     У таблиці наведено деякі числові множини, їх позначення, зображення на координатній прямій і запис у вигляді нерівності.

Завдання:  № 140,142,149