8 клас Геометрія 2022-2023
24.05. Повторення. Чотирикутники та їх площі.
17.05.,19.05 Повторення. Згадуємо самі важливі теми. 12.05. Контрольна робота Контольну виконуємо протягом дня. Бажаю успіхів! КР № 5 Многокутники. Площі многокутників
1. Знайдіть площу паралелограма, одна зі сторін якого дорівнює 9 см, а висота, проведена до неї, – 4 см. 2. Площа трикутника дорівнює 45 см2, а одна з його сторін – 18 см. Знайдіть висоту трикутника, проведену до цієї сторони. 3. Площа трапеції дорівнює 24 см2, а одна з її основ – 5 см, а висота – 4 см. Знайдіть другу основу трапеції. 4. Знайдіть площу ромба, одна з діагоналей якого дорівнює 24 см, а сторона – 13 см. 5. Знайдіть площу паралелограма зі сторонами 8 м і 12 м та гострим кутом 30°. 6. Знайдіть площу рівнобедреної трапеції з основами 12 см і 22 см і бічною стороною 13 см.
10.05. Підготовка до контрольної роботи.Онлайн урок о 8.45. ст.201. Завд.для перевірки знань: №3,5,6 Сторона ромба дорівнює 12 см, а одна з діагоналей - 18 см. Знайдіть площу ромба.д/з. № 8(ст.201)
05.05. Розв'язування задач на знаходження площ фігур. Перегляньте відео:Згадайте основні види та властивості трапеції.Розв'яжіть №1007, 103703.05.Розв'язування задач на знаходження площ фігур.Онлайн урок о 8.45. 323 692 8986Код 0701 Класна робота:318,320,321,323,324,328 (Збірник)Д/з № 319. ст.64(Збірник).
Розв'язуємо задачі зі збірника Розв'язування задач.
Онлайн урок о 11.15. 323 692 8986Код 0701 Д/З № 998
26.04.Площа трапеції.Розв'язування задач.Онлайн урок о 8.45. 323 692 8986Код 0701 1.Повторіть формулу для обчислення площі трапеції.Розв'язуємо задачі із підручника Геометрія. 8 клас№774,776, 777,779,780,781Д/З № 997
21.04.Площа трапеції.Онлайн урок о 11.15. Класна робота: № 986,988,990,993Домашня робота: Вивчити теорему про площу трапеції. №989,991
19.04. Площа трапеції.Онлайн урок о 8.45. Домашня робота: Вивчити теорему про площу трапеції. №979,983
14.04.САМОСТІЙНА РОБОТА.Онлайн урок з алгебри о 11.15. (за 13.04)323 692 8986Код 0701 Самостійна робота1. Знайдіть площу трикутника, з основою 12 см і висотою проведеною до більшої сторони 8 см.
2. Обчисліть площу прямокутного трикутника з гіпотенузою 10см і катетом 6 см.
3.Знайдіть площу ромба з діагоналями 10 см і 20 см;
4. Знайти площу трикутника, якщо сторони трикутника 8см і 14см, а кут між ними 30°
5. Площа трикутника дорівнює 84 см2, а одна з його сторін - 8 см. Знайдіть висоту трикутника, проведену до цієї сторони.ВИКОНАТИ ДО КІНЦЯ ДНЯ!
12.04.Площа трикутника.Онлайн урок о 8.45.
07.04. Площа трикутника.Онлайн урок о 11.15. 323 692 8986Код 0701 Розв'язуємо задачі:1.Знайдіть площу:а) рівнобедреного трикутника з основою 10 см і бічною стороною 13 см;б) трикутника ABC, в якому АВ = 17 см, а висота ВН ділить сторону АС на відрізки АН = 8 см і НС = 2 см.2.Знайдіть площу ромба, діагоналі якого дорівнюють 8 м і 20 м.3. Знайдіть площу прямокутного трикутника, гіпотенуза якого ділиться висотою на відрізки завдовжки 9 см і 4 см.4.Знайдіть площу гострокутного трикутника ABC з висотою AN = 4 см, якщо ВН = 2 см. C = 45°.5.Знайдіть діагоналі ромба, якщо одна з них удвічі більша за другу, а площа ромба дорівнює 64 см2.Д/з. № 953, 956
05.04. Площа трикутника.Онлайн урок о 8.45. Д/З. № 945,949
24.03.Площа паралелограма.Перегляньте відео. Виконайте вправи № 924,926, 928
22.03.Площа паралелограма.Онлайн урок о 8.45. 323 692 8986Код 0701Запам'ятай!
Класна робота:913,915,917,919,921Д/З. 920,922
17.03. Площі многокутників.Розв'язуємо задачі на знаходження площ прямокутника та квадрата(задачі, які зустрічаються в ДПА, ЗНО, НМТ).Класна робота: №886,887,889,897,899,900, 901Д/З. №888,902.
Онлайн урок о 11.15.
15.03.Многокутник і його елементи. Площа многокутника.Онлайн урок о 8.45. 323 692 8986Код 0701Повторюємо №857,859,874,875,877,880,882,883Д/з. № 879,884
10.03. Многокутник і його елементи.Ми розпочинаємо вивчати останній розділ геометрії в цьому році. Присвячений він многокутникам. 1. Опрацюй матеріал підручника п. 22Запам'ятай:Класна робота №841,842, 845,847,849,851Д/З №850,852
08.03. Контрольна робота з теми " Розв'язуваня прямокутних трикутників"Перед виконанням завдань повторіть теорему Піфагора, означення синуса, косинуса, тангенса. Покладіть перед собою таблицю квадратів чисел та значення синусів,косинусів та тангенсів гостого кута. Контольну виконуємо протягом дня. Бажаю успіхів!
03.03.2023. Підготовка до контрольної роботи.Онлайн урок о 11.20.323 692 8986Код 0701Класна робота :ст.163 (домашня самостійна робота) № 1,3,5,10. Завдання для перевірки знань (3,4,6,8). Домашня робота:№ 826
01.03.2023. Розв'язування прямокутних трикутників.
Онлайн урок о 12.20.323 692 8986Код 0701
24.02.2023. Розв'язування прямокутних трикутників.Онлайн урок о 11.15.(дист.група), 12.20. (змішана група)Д/з. № 785(3,4), 78922.02.17.02. Співвідношення міх сторонами та кутами прямокутного трикутника.Означення: синуса, косинуса, тангенса та котангенса гострого кута! Онлайн урок о 8.45.(дист.група), 12.20. (змішана група)323 692 8986Код 0701Класна робота№2.Діагональ прямокутника дорівнює 85 см і утворює зі стороною кут 65°. Знайдіть сторони прямокутника.
Д/З §20(повторити означення), розв'язати задачу№1. Дерево заввишки 20 м, що росте на одному березі річки, з другого
берега видно під кутом 15°. Знайдіть ширину річки. (Припускаємо,
що основа дерева і око спостерігача — на одному рівні.)
17.02. Співвідношення міх сторонами та кутами прямокутного трикутника.Вивчіть означення: синуса, косинуса, тангенса та котангенса гострого кута! Онлайн урок о 11.20.323 692 8986Код 0701Класна робота:№ 740, 742,744,746.
Д/З §20(повторити означення),№743,747(1,2,3).
15.02.Тема. Синус, косинус, тангенс та котангенс гострого кута.Онлайн урок о 8.50.323 692 8986Код 07011. Опрацюй матеріал підручника п. 20Згадай поняття гострого кута, прилеглого катета, протилежного катета, гіпотенузи. Вивчи означення :синус, косинус, тангенс та котангенс гострого кута. Вивчи таблицю :3. Виконай в зошитах: №737, 738,750, 740, 742
Д/З §20(вивчити означення),№739,751.
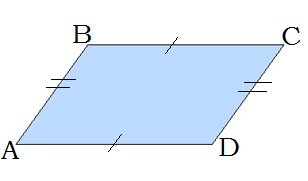
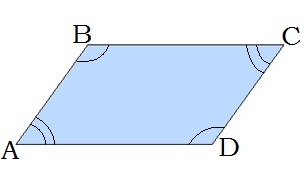
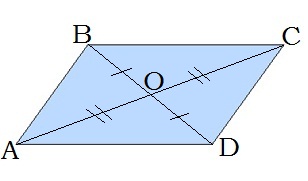
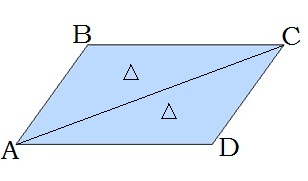
24.05. Повторення. Чотирикутники та їх площі.
17.05.,19.05 Повторення. Згадуємо самі важливі теми.
12.05. Контрольна робота
Контольну виконуємо протягом дня. Бажаю успіхів!
КР № 5 Многокутники. Площі многокутників
1. Знайдіть площу паралелограма, одна зі сторін якого дорівнює 9 см, а висота, проведена до неї, – 4 см.
2. Площа трикутника дорівнює 45 см2, а одна з його сторін – 18 см. Знайдіть висоту трикутника, проведену до цієї сторони.
3. Площа трапеції дорівнює 24 см2, а одна з її основ – 5 см, а висота – 4 см. Знайдіть другу основу трапеції.
4. Знайдіть площу ромба, одна з діагоналей якого дорівнює 24 см, а сторона – 13 см.
5. Знайдіть площу паралелограма зі сторонами 8 м і 12 м та гострим кутом 30°.
6. Знайдіть площу рівнобедреної трапеції з основами 12 см і 22 см і бічною стороною 13 см.
10.05. Підготовка до контрольної роботи.
Онлайн урок о 8.45.
ст.201. Завд.для перевірки знань: №3,5,6
Сторона ромба дорівнює 12 см, а одна з діагоналей - 18 см. Знайдіть площу ромба.
д/з. № 8(ст.201)
05.05. Розв'язування задач на знаходження площ фігур.
Перегляньте відео:
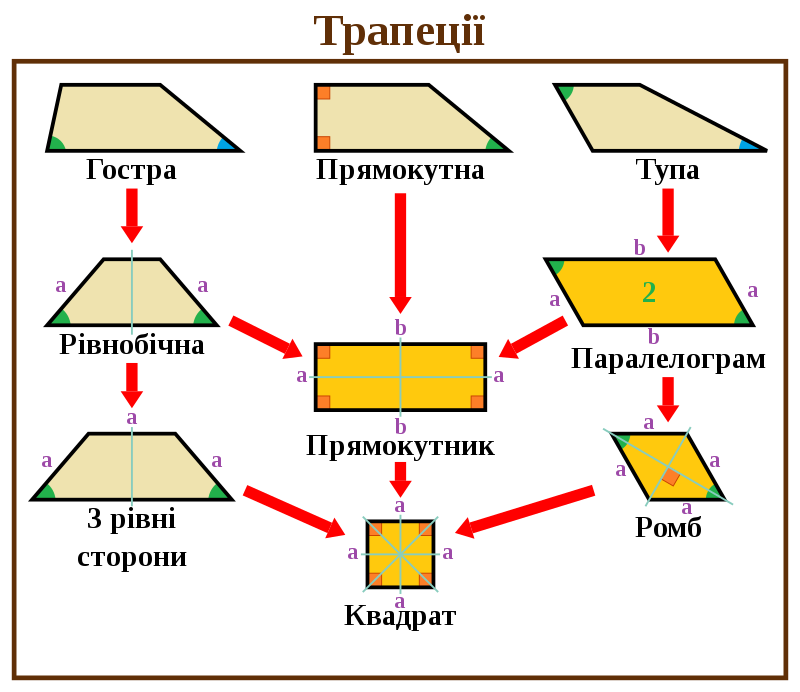
Згадайте основні види та властивості трапеції.
Розв'яжіть №1007, 1037
03.05.Розв'язування задач на знаходження площ фігур.
Онлайн урок о 8.45.
323 692 8986
Код 0701
Класна робота:318,320,321,323,324,328 (Збірник)
Д/з № 319. ст.64(Збірник).
Розв'язуємо задачі зі збірника Розв'язування задач.
Онлайн урок о 11.15.
323 692 8986
Код 0701
Д/З № 998
26.04.Площа трапеції.Розв'язування задач.
Онлайн урок о 8.45.
323 692 8986
Код 0701
1.Повторіть формулу для обчислення площі трапеції.
Розв'язуємо задачі із підручника Геометрія. 8 клас
№774,776, 777,779,780,781
Д/З № 997
21.04.Площа трапеції.
Онлайн урок о 11.15.
Класна робота: № 986,988,990,993
Домашня робота: Вивчити теорему про площу трапеції. №989,991
19.04. Площа трапеції.
Онлайн урок о 8.45.
Домашня робота: Вивчити теорему про площу трапеції. №979,983
14.04.САМОСТІЙНА РОБОТА.
Онлайн урок з алгебри о 11.15. (за 13.04)
323 692 8986
Код 0701
Самостійна робота
2. Обчисліть площу прямокутного трикутника з гіпотенузою 10см і катетом 6 см.
3.Знайдіть площу ромба з діагоналями 10 см і 20 см;
4. Знайти площу трикутника, якщо сторони трикутника 8см і 14см, а кут між ними 30°
5. Площа трикутника дорівнює 84 см2, а одна з його сторін - 8 см. Знайдіть висоту трикутника, проведену до цієї сторони.
ВИКОНАТИ ДО КІНЦЯ ДНЯ!
12.04.Площа трикутника.
Онлайн урок о 8.45.
07.04. Площа трикутника.
Онлайн урок о 11.15.
323 692 8986
Код 0701
Розв'язуємо задачі:
1.Знайдіть площу:
а) рівнобедреного трикутника з основою 10 см і бічною стороною 13 см;
б) трикутника ABC, в якому АВ = 17 см, а висота ВН ділить сторону АС на відрізки АН = 8 см і НС = 2 см.
2.Знайдіть площу ромба, діагоналі якого дорівнюють 8 м і 20 м.
3. Знайдіть площу прямокутного трикутника, гіпотенуза якого ділиться висотою на відрізки завдовжки 9 см і 4 см.
4.Знайдіть площу гострокутного трикутника ABC з висотою AN = 4 см, якщо ВН = 2 см. C = 45°.
5.Знайдіть діагоналі ромба, якщо одна з них удвічі більша за другу, а площа ромба дорівнює 64 см2.
Д/з. № 953, 956
05.04. Площа трикутника.
Онлайн урок о 8.45.
Д/З. № 945,949
24.03.Площа паралелограма.
Перегляньте відео.
Виконайте вправи № 924,926, 928
22.03.Площа паралелограма.
Онлайн урок о 8.45.
323 692 8986
Код 0701
Запам'ятай!
Класна робота:913,915,917,919,921Д/З. 920,922
17.03. Площі многокутників.
Розв'язуємо задачі на знаходження площ прямокутника та квадрата(задачі, які зустрічаються в ДПА, ЗНО, НМТ).
Класна робота: №886,887,889,897,899,900, 901
Д/З. №888,902.
Онлайн урок о 11.15.
15.03.Многокутник і його елементи. Площа многокутника.
Онлайн урок о 8.45.
323 692 8986
Код 0701
Повторюємо №857,859,874,875,877,880,882,883Д/з. № 879,884
10.03. Многокутник і його елементи.
Ми розпочинаємо вивчати останній розділ геометрії в цьому році. Присвячений він многокутникам.
1. Опрацюй матеріал підручника п. 22
Запам'ятай:
Класна робота №841,842, 845,847,849,851
Д/З №850,852
08.03. Контрольна робота з теми " Розв'язуваня прямокутних трикутників"
Перед виконанням завдань повторіть теорему Піфагора, означення синуса, косинуса, тангенса. Покладіть перед собою таблицю квадратів чисел та значення синусів,косинусів та тангенсів гостого кута. Контольну виконуємо протягом дня. Бажаю успіхів!
03.03.2023. Підготовка до контрольної роботи.
Онлайн урок о 11.20.
323 692 8986
Код 0701
Класна робота :ст.163 (домашня самостійна робота) № 1,3,5,10. Завдання для перевірки знань (3,4,6,8).
Домашня робота:№ 826
01.03.2023. Розв'язування прямокутних трикутників.
Онлайн урок о 12.20.
323 692 8986
Код 0701
24.02.2023. Розв'язування прямокутних трикутників.
Онлайн урок о 11.15.(дист.група), 12.20. (змішана група)
Д/з. № 785(3,4), 789
22.02.17.02. Співвідношення міх сторонами та кутами прямокутного трикутника.
Означення: синуса, косинуса, тангенса та котангенса гострого кута!
Онлайн урок о 8.45.(дист.група), 12.20. (змішана група)
323 692 8986
Код 0701
Класна робота
№2.Діагональ прямокутника дорівнює 85 см і утворює зі стороною кут 65°. Знайдіть сторони прямокутника.
Д/З §20(повторити означення), розв'язати задачу
№1. Дерево заввишки 20 м, що росте на одному березі річки, з другого
берега видно під кутом 15°. Знайдіть ширину річки. (Припускаємо,
що основа дерева і око спостерігача — на одному рівні.)
17.02. Співвідношення міх сторонами та кутами прямокутного трикутника.
Вивчіть означення: синуса, косинуса, тангенса та котангенса гострого кута!
Онлайн урок о 11.20.
323 692 8986
Код 0701
Класна робота:№ 740, 742,744,746.
Д/З §20(повторити означення),№743,747(1,2,3).
15.02.Тема. Синус, косинус, тангенс та котангенс гострого кута.
Онлайн урок о 8.50.
323 692 8986
Код 0701
1. Опрацюй матеріал підручника п. 20
Згадай поняття гострого кута, прилеглого катета, протилежного катета, гіпотенузи.
Вивчи означення :
синус, косинус, тангенс та котангенс гострого кута.
Вивчи таблицю :
3. Виконай в зошитах: №737, 738,750, 740, 742
Д/З §20(вивчити означення),№739,751.
10.02.Самостійна робота
10.02.Самостійна робота
Виконуємо самостійну роботу до 14.02.Заходимо під своїм прізвищем, записуємо лише відповідь.Термін виконання с/р закінчився.
Виконуємо самостійну роботу до 14.02.
Заходимо під своїм прізвищем, записуємо лише відповідь.
Термін виконання с/р закінчився.
03,08.02.2023.Перпендикуляр і похила, їхні властивості.
Онлайн урок о 8.50.
323 692 8986
Код 0701
Перегляньте відео:
Опрацюйте § 19. Вивчіть властивості перпендикуляра і похилої.
Класна робота № 710,714,716,718
Домашня робота № 715,717
01.02.2023.Теорема Піфагора. Розв'язування задач.
Онлайн урок о 8.50.
323 692 8986
Код 0701
Виконуємо на уроці: № 675,676, 677,679
Д/з: §18. Повторити теорему. №678,680
27.01.2023.Теорема Піфагора. Розв'язування задач.
Виконуємо на уроці: № 654, 656, 658, 660,662
Д/з: §18. Повторити теорему. №659,663
25.01.2023. Теорема Піфагора.
Одна з найвідоміших геометричних теорем — теорема Піфагора, знаменитого давньогрецького філософа і математика.
В історії математики знаходимо твердження, що цю теорему знали за багато років до Піфагора, наприклад, стародавні єгиптяни знали про те, що трикутник зі сторонами 3 , 4 і 5 є прямокутним.
ЗАПАМʼЯТАЙТЕ!
Д/з: §18. Вивчити теорему. №653,655
























 .
. .
.

 .
.








Комментарии
Отправить комментарий