8 клас Алгебра дистанційне навчання 2019/2021
05.05.Рівняння, які зводяться до квадратних. Біквадратні рівняння.
Завдання. № 803, 813
28.04.Дробово-раціональні рівняння, які зводяться до квадратних
Zoom. 10:15Подключиться к конференции Zoom
Идентификатор конференции: 775 7510 7747Код доступа: 2804
Завдання:параграф 3, п.24. № 797, 799, 801.
26.04.Розв'язування вправ.Згадуємо правила розв'язання квадратних рівнянь.Виконуємо:№953,954
21.04.Квадратний тричлен. Розв'язування вправ.1.Згадайте правила розкладання квадратного тричлена на множника.
2. Виконайте:№780
19.04.Квадратний тричленОнлайн урок. : 19.04. 2021 10:15 ІД: 731 1534 1245Код: 1919
Перегляньте відеоЗапам'ятайте:Квадратним тричленом називається многочлен вигляду ax2 + bx + c, де x — змінна, a, b і c — деякі числа-коефіцієнти, при цьому a ≠ 0. Коренями квадратного тричлена називаються числа, при яких тричлен дорівнює нулю.Отже, щоб знайти корені квадратного тричлена, треба скласти відповідне йому квадратне рівняння (у лівій частині даний тричлен, у правій — нуль) і розв’язати його. Корені квадратного рівняння будуть коренями відповідного квадратного тричлена.
Якщо числа x1 і x2 є коренями деякого квадратного тричлена, то його можна розкласти на три множники, один із яких є першим коефіцієнтом тричлена при x2, а два інші є різницею змінної x і кожного з коренів тричлена: ax2 + bx + c = a(x - x1)(x - x2).
Якщо квадратний тричлен має один корінь, то його можна розкласти на множники, один із яких є першим коефіцієнтом, а другий є квадратом різниці змінної x і кореня тричлена: ax2 + bx + c = a(x - x1)2.
Якщо тричлен коренів не має, то його не можна розкласти на лінійні множники.
Виконаємо разом: №775,778
Домашнє завдання: № 776,779
14.04.Контрольна робота з теми: "Квадратні рівняння"
👉Посилання на к/р (оцінки будуть після перевірки)
12.04. Підготовка до контрольної роботи з теми: "Квадратні рівняння"Онлайн урок: 12 апр. 2021 10:15 AM Киев
Підключитися
ІД: 748 4198 8890Код: 1212
Приклад контрольної роботи
1. Розв’яжіть рівняння: (1 бал) x2 - 16 = 0
2. 2. Знайдіть всі корені рівняння: (1 бал) x2 - 5x = 0
3. 3.Знайдіть дискримінант квадратного рівняння: (1 бал) 3x2 - x - 5 =0
4. Знайдіть всі корені рівняння: (1 бал) 5x2 - 6x +1 =0
5. Знайдіть суму та добуток коренів квадратного рівняння: (2 бал)
x2 + 3x - 40 =0
6. Застосовуючи теорему, обернену до теореми Вієта, розв’яжіть рівняння: (2 бал)
x2 - 5x + 6 =0
7. Один із коренів квадратного рівняння дорівнює 3. Знайдіть другий корінь рівняння: (2 бали)
x2 - 2x - 3 =0
8. Знайдіть, при якому значенні а рівняння має єдиний корінь. Знайдіть цей корінь. (2 бали)
07.04. Квадратні рівняння.Виконайте: Самостійна робота
05.04. Розв'язування рівнянь за допомогою теореми Вієта.Повторюємо теорему Вієта .Виконуємо № 757Домашнє завдання: № 758
Урок 8-а: 5.04. 2021 09:15
Ід: 787 5557 2836Код: 0504
Тетяна Садовенко приглашает вас на запланированную конференцию: Zoom.
Урок: 8-б Время: 5.04. 2021 10:00
Підключитися:
ІД: 732 2316 9432Код: 5040
29.03. Теорема Вієта.
Приклад контрольної роботи
1. Розв’яжіть рівняння: (1 бал) x2 - 16 = 0
2. 2. Знайдіть всі корені рівняння: (1 бал) x2 - 5x = 0
3. 3.Знайдіть дискримінант квадратного рівняння: (1 бал) 3x2 - x - 5 =0
4. Знайдіть всі корені рівняння: (1 бал) 5x2 - 6x +1 =0
5. Знайдіть суму та добуток коренів квадратного рівняння: (2 бал)
x2 + 3x - 40 =0
6. Застосовуючи теорему, обернену до теореми Вієта, розв’яжіть рівняння: (2 бал)
x2 - 5x + 6 =0
7. Один із коренів квадратного рівняння дорівнює 3. Знайдіть другий корінь рівняння: (2 бали)
x2 - 2x - 3 =0
8. Знайдіть, при якому значенні а рівняння має єдиний корінь. Знайдіть цей корінь. (2 бали)
Завдання: №736, 740
24.03.Розв'язування квадратних рівнянь.1.Згадайте:Формула коренів квадратного рівняння
Дискримінантом квадратного рівняння називається вираз, що дорівнює різниці квадрата другого коефіцієнта і добутку першого коефіцієнта та вільного члена, помноженого на чотири. Дискримінант позначається великою латинською буквою D : D = b2 - 4ac.
Корені повного квадратного рівняння знаходять за формулою  .
.
Якщо дискримінант квадратного рівняння додатний, то рівняння має два корені.
Якщо дискримінант квадратного рівняння дорівнює нулю, то рівняння має один корінь, який дорівнює другому коефіцієнту, узятому з протилежним знаком і поділеному на подвоєний перший коефіцієнт:  .
.
Якщо дискримінант квадратного рівняння від’ємний, то рівняння не має коренів.
2. Розв'яжіть:
Формула коренів квадратного рівняння
Дискримінантом квадратного рівняння називається вираз, що дорівнює різниці квадрата другого коефіцієнта і добутку першого коефіцієнта та вільного члена, помноженого на чотири. Дискримінант позначається великою латинською буквою D : D = b2 - 4ac.
Корені повного квадратного рівняння знаходять за формулою .
Якщо дискримінант квадратного рівняння додатний, то рівняння має два корені.
Якщо дискримінант квадратного рівняння дорівнює нулю, то рівняння має один корінь, який дорівнює другому коефіцієнту, узятому з протилежним знаком і поділеному на подвоєний перший коефіцієнт: .
Якщо дискримінант квадратного рівняння від’ємний, то рівняння не має коренів.

Неповні квадратні рівняння
Згідно з означенням, перший коефіцієнт квадратного рівняння не може дорівнювати нулю: якщо  , то
, то  перетворюється у лінійне рівняння
перетворюється у лінійне рівняння 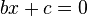 . Якщо хоч один коефіцієнт
. Якщо хоч один коефіцієнт  або
або  дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів:
дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів: ;
; 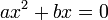 ;
; 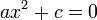 .
.
Згідно з означенням, перший коефіцієнт квадратного рівняння не може дорівнювати нулю: якщо  , то , то  перетворюється у лінійне рівняння перетворюється у лінійне рівняння 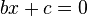 . Якщо хоч один коефіцієнт . Якщо хоч один коефіцієнт  або або  дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів: дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів:
|
Розв'язування неповних квадратних рівнянь
20.01. Розв'язування вправ.
1. Згадайте: Квадра́тний ко́рінь з числа x — це число, квадрат якого дорівнює x.
2. Виконайте вправи: № 70,71👇
18.01. Арифметичний квадратний корінь. Розв'язування вправ.1.Онлайн урок 10:30 Подключитися Ід: 723 5488 0934Код доступа: 1881
2.Д/з 434,442 або № 447(високий рівень)
3. Виконайте ТЕСТ (до 20.01.)
13.01.Арифметичний квадратний корінь.
8-аВремя: 13 янв. 2021 09:30 AM Киев
Идентификатор конференции: 759 8626 6190Код доступа: 1313
8-бВремя: 13 янв. 2021 10:30 AM Киев
Идентификатор конференции: 779 6238 4494Код доступа: 1331
11.01. Функція y=х2 Time: Jan 11, 2021 09:35
Meeting ID: 777 3587 9211Passcode: 1212
Д/з. № 397,399,401
23.12. Повторення. Стандартний вигляд числа.
21.12. Повторення. Функція обернена пропорційність.16.11Тетяна Садовенко приглашает вас на запланированную конференцию: Zoom.
Тема: Алгебра 8-БВремя: 16 ноя 2020 10:30 AM Киев
Подключиться к конференции Zoomhttps://us04web.zoom.us/j/72964697845?pwd=SExUeUYzMmdpdVRNQ3RuMWdNR204dz09
Идентификатор конференции: 729 6469 7845Код доступа: 1116
02.11.Тетяна Садовенко приглашает вас на запланированную конференцию: Zoom.
Тема: 8 клас Тетяна СадовенкоВремя: 2 ноя 2020 09:15 AM Киев
Подключиться к конференции Zoomhttps://us04web.zoom.us/j/75924470286?pwd=MEQzNEJmNXllN2JscVRPbDhvVUd6UT09
Идентификатор конференции: 759 2447 0286Код доступа: 1111
- знаменники всіх дробів розкладаються на множники (якщо це необхідно та можливо);
- з одного знаменника беруться всі множники, а з інших тільки ті, яких немає в першому знаменнику (тобто ті, яких «бракує»).
Аби безпомилково визначити додатковий множник для кожного дробу, отриманий спільний знаменник краще одразу записати в знаменнику «нового» дробу.
21.05.-25.05. Контрольна робота з теми "Квадратні рівняння "
18.05.-20.05.Розвязування задач за допомогою квчадратних рівнянь.
Параграф 3, п.25. № 828,830,834
12.05.-15.05.Рівняння, які зводяться до квадратних. Біквадратні рівняння.
Тема: Конференція Zoom. Біквадратні рівняння.
Время: 13 травня 2020 12:00
Идентификатор конференции: 323 692 8986
Пароль: 6LCSUR

Завдання:параграф 3, п.24. № 797, 799, 801.
27.04.-30.04.Квадратний тричлен
завдання:ст.182-184. № 775,778,780, 783
16.04.-24.04. Теорема Вієта.
завдання: №736, 737

07.04. - 15.04.
Самостійна робота
Домашнє завдання: № 706, 715 ( Підказка: Ці рівняння спочатку потрібно звести до квадратних, а потім розв"язати) - чекаю у VIBER
З0.03.- 07.04.
Формули коренів квадратного рівняння
Опрацювати параграф 3.п.21. № 702, 703,704, 711
Про неповні квадратні рівняння (відео)
Неповні квадратні рівняння
Згідно з означенням, перший коефіцієнт квадратного рівняння не може дорівнювати нулю: якщо  , то , то  перетворюється у лінійне рівняння перетворюється у лінійне рівняння 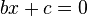 . Якщо хоч один коефіцієнт . Якщо хоч один коефіцієнт  або або  дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів: дорівнює нулю, то квадратне рівняння називається непо́вним. Неповні квадратні рівняння бувають трьох видів:
Розв'язування неповних квадратних рівнянь
Приклад. Розв’яжіть рівняння:  Розв’язання. |
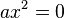 рівносильне рівнянню
рівносильне рівнянню  і тому завжди має тільки один корінь
і тому завжди має тільки один корінь  .
.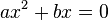 розв'язується винесенням за дужки
розв'язується винесенням за дужки  :
:  . Таке рівняння має два корені:
. Таке рівняння має два корені: 
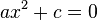 рівносильне рівнянню
рівносильне рівнянню  . Якщо
. Якщо  , воно має два дійсних розв'язки, якщо
, воно має два дійсних розв'язки, якщо 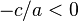 — жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то
— жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то 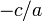 - додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число
- додатне і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число 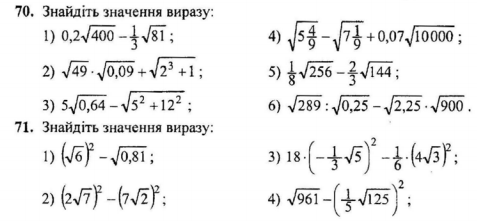


Комментарии
Отправить комментарий